Vektor (Timara Oliviaputie /24)

Vektor
1.   Pengertian Vektor
·      Vektor adalah himpunan garis berarah yang mempunyai panjang dan arah atau sesuatu yang mempunyai besaran dan arah.
·      Skala adalah sesuatu yang hanya mempunyai besaran saja.
·      Vektor dengan titik pangkal A dan ujungnya B ditulis  bisa juga ditulis dengan .


a.    Vektor Posisi
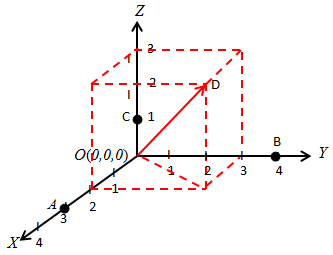
Adalah vektor yang titik pangkalnya di titik pusat koordinat.Hasil gambar untuk vektor posisi




b.    Cara Menulis Vektor
Bentuk
2 Dimensi
3 Dimensi
Baris
(x,y)
(x,y,z)
Kolom
Gambar terkait
Basis
xi+yj
xi+yj+zk

c.    Vektor Negatif

Hasil gambar untuk vektor kolom
Adalah vektor yang arahnya berlawanan arah vektor positif.
Hasil gambar untuk pertambahan vektor matematika
a.    Panjang Vektor
Panjang anak panah (ruas garis) menyatakan besarnya vektor (modulus).
Hasil gambar untuk panjang vektor
Contoh soal:
1.    jika=, tentukan panjang
Jawab:
       = =  = 5
2.    Jika A(1,0) dan B(4,3), tentukan panjang vektor
Jawab:
       ==
  =   = 3 

b.    Kesamaan Dua Vektor
2 buah vektor a=(a1,a2) dan b=(a1,a2) dikatakan sama & dinotasikan a=b, jika a1=b1 dan a2=b2. Maka memiliki panjang & arah yang sama.

c.    Penjumlahan dan Pengurangan Vektor
Secara Aljabar
Penjumlahan & pengurangan 2 buah vektor a=(a1,a2) dan b=(b1,b2) dalam R kuadrat didefinisikan sebagai berikut.
a+b= (a1,a2) + (b1,b2) =(a1 + b1,a2 + b2)
a-b=(a1,a2) - (b1,b2) = (a1 - b1,a2 - b2)

Contoh soal:
1.    jika =;=; =, tantukan panjang = +-
Jawab:
= +-
   = +-
   =
= = = 3

Secara Geometri
untuk mencari penjumlahan dan pengurangan dari beberapa vektor, dapat dilakukan dengan beberapa aturan berikut.





Metode Ujung ke Pangkal (tip-to-tail method)Hasil gambar untuk pertambahan vektor matematika
Metode Jajargenjang
Hasil gambar untuk pertambahan vektor matematika metode jajargenjang 

d.    Perkalian Vektor
Setiap a=(a1,a2) dalam R kuadrat & sebuah skalar n elemen R maka
na=n(a1,a2)=(na1,na2)
         Jika n>0, maka na searah dengan a

         Jika n<0, maka na berlawanan arah dengan a




Soal Latihan :
1. Diketahui segitiga PQR dengan P(0,1,4),Q(2,-3,2), dan R(-1,0,2). besar sudut PQR=...
2. Diketahui A(4,9,1), B(6,3,-2), dan C(-2,6,3) adalah titik-titik sudut segitiga. Luas segitiga  
    ABC adalah...
3. Diketahui vektor a=(1,2,-3) dan vektor b=(2,-1,2). tentukan luas jajar genjang tersebut...
4. Jika A(1,0) dan B(4,3), tentukan panjang vektor AB!
5. Segitiga PQR memiliki titik sudut P(2,-3,4), Q(6,-2,2) dan R(5,4,3). Proyeksi orthogonal vektor PR pada PQ diwakili oleh vektor...

Komentar

  1. Unknown22 Oktober 2017 pukul 07.46

    p = QR = √[(-1 - 2)² + (0 + 3)² + (2 - 2)²] = 3√2 ---> p² = 18
    q = PR = √[(-1 - 0)² + (0 - 1)² + (2 - 4)²] = √6 ------> q² = 6
    r = PQ = √[(2 - 0)² + (-3 - 1)² + (2 - 4)²] = 2√6 -----> r² = 24

    aturan cosinus
    cos ∠PQR = (p² + r² - q²)/(2pq)
    cos ∠PQR = (18 + 24 - 6)/(2 × 3√2 × 2√6)
    cos ∠PQR = 36/(12√12)
    cos ∠PQR = ½√3

    sehingga ∠PQR = 30°

    Saffanah Janan (21)

    BalasHapus

Posting Komentar

Postingan populer dari blog ini

Fungsi, Komposisi Fungsi, Fungsi invers, dan Grafik Fungsi oleh Allamanda (03)

Gambar
A. Fungsi Fungsi, atau disebut juga pemetaan, merupakan sebuah relasi yang khusus.  Fungsi/pemetaan  dari himpunan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota A, dengan tepat satu anggota B. Dengan demikian, setiap anggota himpunan A mempunyai tepat satu kawan dengan anggota himpunan B. Jadi, fungsi sudah pasti sebuah relasi, tetapi relasi belum tentu sebuah fungsi. Misalkan  f  adalah suatu fungsi yang memetakan  x  anggota A ke  y  anggota B, maka fungsi  f  dapat dinotasikan sebagai berikut:    Aljabar Fungsi Sebelum membahas komposisi fungsi, mari mengulang lagi tentang sifat-sifat fungsi aljabar. Jika f(x) dan g(x) adalah fungsi-fungsi aljabar yang terdefinisi, maka berlaku sifat-sifat fungsi aljabar berikut. 1. (f + g)(x) =  f(x) + g(x) 2. (f - g)(x) =  f(x) - g(x) 3. (f . g)(x) =  f(x) . g(x) 4. (f /g)(x) =  f(x) / g(x) , g(x) tidak sama dengan...
Baca selengkapnya

Pertumbuhan dan Peluruhan (Vera Amelia Santoso 25)

Pertumbuhan dan Peluruhan Pertumbuhan   = bertambah Peluruhan        = berkurang Pertumbuhan : meningkatnya jumlah suatu benda Rumus :         Pn = Po (1+r) n     Keterangan : n           : waktu Pn        : jumlah pada waktu n Po         : jumlah awal r           : kenaikan (presentase atau bagian) Contoh soal : 1)      Seorang petani mencatat hasil panennya 5 tahun terakhir. Ternyata, disimpulkan bahwa hasil panen dari tahun ke tahun bertambah 20%. Jika pada pertama kali, jumlah panen 10 ton, tentukan hasil panen pada 4 tahun berikutnya! Jawab : 20% = 0,2 r = 0,2 n = 4 Po = 10 ton P 4 = 10 (1+0,2) 4      = 10 (1,2) 4      = 10 (2,0736) ...
Baca selengkapnya

LIMIT FUNGSI ALJABAR (Saffanah Janan 21)

Gambar
A. Pengertian Limit fungsi aljabar  adalah suatu nilai pendekatan disekitar titik tertentu baik pendekatan dari kiri suatu titik maupun pendekatan dari kanan titik tersebut  (Dedi Heryadi, 2007). B. Bentuk Ada 2 bentuk dalam menentukan limit fungsi aljabar yaitu : Bentuk pertama Bentuk kedua Dalam kaitanya dengan bentuk limit pertama  ada beberapa metode didalam menentukan nilai limit fungsi aljabar yaitu dengan metode subsitusi dan metode pemfaktoran. C. Metode 1. Subsitusi : Metode subsitusi digunakan apabila dalam hasil perhitungan tidak diperoleh  bentuk tak tentu seperti 0/0, ∞ /∞ , ∞ -∞   Contoh (1) : Contoh (2) : Contoh (3) : Contoh (4) : Contoh (5) : Contoh (6) : Contoh (7) : 2. Pemfaktoran atau Faktorisasi Jika dengan cara subtitusi diperoleh bentuk tak tentu 0/0 atau maka perhitungan nilai limit dilakukan dengan cara   memfaktorkan Contoh (1) : Contoh (2) : ...
Baca selengkapnya