Persamaan Lingkaran dan Garis Singgung Lingkaran (Naurah Aurel 16)
Persamaan Lingkaran
Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak sama terhadap suatu titik tertentu. Titik tertentu itu disebut pusat lingkaran, sedangkan jarak titik terhadap pusat lingkaran disebut jari-jari lingkaran.
Gambar dibawah ini menunjukkan lingkaran dengan pusat P dan jari-jari r.
1. Persamaan lingkaran yang berpusat O (0, 0) dan jari-jari r
Pada lingkaran disamping jari-jari atau r = OP, OQ = x dan PQ = y.
Jarak dari O (0, 0) ke P (x, y) adalah.
Berdasarkan rumus Pythagoras
Jadi persamaan lingkaran dengan pusat O (0, 0) dan jari-jari r adalah x2 + y2 = r2
Contoh :
Tentukan persamaan lingkaran yang berpusat O (0, 0) dan jari-jari 5
Jawab :
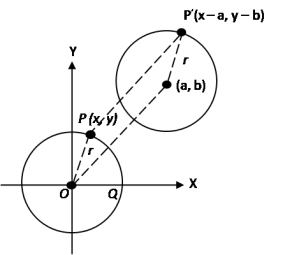
2. Persamaan lingkaran yang berpusat P (a, b) dan berjari-jari r
Persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r dapat diperoleh dari persamaan lingkaran yang berpusat di (0, 0) dan berjari-jari r dengan menggunakan teori pergeseran. Jika pusat (0, 0) bergeser (a, b) maka titik (x, y) bergeser ke (x + a, y + b).
Diperoleh persamaan.
Persamaan lingkaran menjadi (x’– a)2 + (y’ – b)2 = r2
Jadi persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah (x- a)2 + (y – b)2 = r2
Contoh 1 :
Tentukan persamaan lingkaran yang berpusat di (3, 2) dan berjari-jari 4
Jawab :
Pusat (3, 2) maka a = 3 dan b = 2
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
(x- 3)2 + (y – 2)2 = 42
(x- 3)2 + (y – 2)2 = 16
Contoh 2 :
Tentukan persamaan lingkaran berpusat di titik P(2, 3) yang melalui Q(5, -1)
Jawab :
Pusat (2, 3) maka a = 2 dan b = 3
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
(x- 2)2 + (y – 3)2 = 252
B. Bentuk umum persamaan lingkaran
Persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah
(x- a)2 + (y – b)2 = r2
x2 – 2ax + a2 + y2 – 2by + b2 = r2
x2+ y2 – 2ax – 2by + a2+ b2– r2 = 0 atau x2+ y2 + Ax + By + a2+ b2+ C= 0
Jadi bentuk umum persamaan lingkaran x2+ y2 + Ax + By + a2+ b2+ C= 0
Contoh :
Tentukan pusat dan jari-jari lingkaran x2+ y2 – 4x +2y – 20= 0
Jawab :
A = -4, B = 2, dan C = -20
B. Kedudukan Titik dan Garis Pada Lingkaran
Kedudukan Titik Pada Lingkaran
Kedudukan Garis Pada Lingkaran
Untuk mengetahui kedudukan/ posisi sebuah garis terhadap lingkaran, substitusikan garis terhadap lingkaran sehingga didapatkan bentuk ax2+bx+c=0.
Letak K (m,n) terhadap X2+Y2 +Ax + By +C= 0 , ditentukan oleh nilai kuasa titik tersebut terhadap lingkaran
nilai kuasa K = m2+n2 +Am + Bn +C,
nilai kuasa K = m2+n2 +Am + Bn +C,
- K < 0
di dalam lingkaran
- K= 0
pada lingkaran
- K > 0
di luar lingkaran
Contoh 1:
Tentukan kedudukan titik-titik berikut terhadap lingkaran X2+y2 -8x -10y +16 =0 dan gambarlah
a. H(-3,9) b L(7,9), c M(10,5), d N(1,7)
Jawaban:Tentukan kedudukan titik-titik berikut terhadap lingkaran X2+y2 -8x -10y +16 =0 dan gambarlah
a. H(-3,9) b L(7,9), c M(10,5), d N(1,7)
- H(-3,9)
K = (-3)2+92 -8.(-3) -10.9 +16 = 40, K > 0, diluar lingkaran
- L(7,9)
K = (7)2+92 -8.(7) -10.9 +16 = 0, K = 0, pada lingkaran
- M(10,5) K = (10)2+52 -8.(10) -10.5 +16 = 11, K > 0, diluar lingkaran
- N(1,7) K = 12+72 -8.(1) -10.7 +16 = -12, K < 0, didalam lingkaran
Contoh 2:
Diketahui sebuah lingkaran X2+y2 -2x +6y -15 =0 dan sebuah titik S(m,1), tentukan batas nilai m agar
Diketahui sebuah lingkaran X2+y2 -2x +6y -15 =0 dan sebuah titik S(m,1), tentukan batas nilai m agar
- titik S didalam lingkaran
- titik S diluar lingkaran
| S(m,1) | = kuasa |
| = m2 +12 - 2m +6.1 - 15 | |
| = m2 - 2m - 8 |
| a. | Syarat di dalam lingkaran, K< 0 m2 -2m -8 <0 (m-4)(m+2)=0 |
| m=-2 atau m=4 | |
| didalam lingkaran jika -2 < m <4 ( daerah - - - ) | |
| diluar lingkaran, K >0, jika m<-2 atau m >4 (daerah ++ ) |
Kedudukan Garis Pada Lingkaran
Untuk mengetahui kedudukan/ posisi sebuah garis terhadap lingkaran, substitusikan garis terhadap lingkaran sehingga didapatkan bentuk ax2+bx+c=0.
Lihat diskriminannya: 
Jika
- D<0, berarti garis berada di luar lingkaran (tidak memotong lingkaran)
- D=0, berarti garis menyinggung lingkaran
- D>0, berarti garis memotong lingkaran di 2 titik berbeda.
Contoh 1:
- Tentukan posisi garis:
terhadap lingkaran
Jawab:
Karena  , maka garis berada di luar lingkaran.
, maka garis berada di luar lingkaran.
Contoh 2:
- Tentukan p agar garis
terletak di luar lingkaran
!
Jawab:
- syarat:
atau
Gambar dengan garis bilangan untuk pertidaksamaan diatas, maka akan didapatkan nilai p:  atau
atau 
C. Persamaan Garis Singgung Lingkaran
Jika persamaan lingkaran  , maka persamaan garis singgungnya:
, maka persamaan garis singgungnya:
Persamaan garis singgung untuk suatu titik (x1,y1) yang terletak pada lingkaran
- Jika persamaan lingkaran
, maka persamaan garis singgungnya:
- Jika persamaan lingkaran berbentuk
, maka persamaan garis singgungnya:
Persamaan lingkaran  dapat juga diubah menjadi
dapat juga diubah menjadi  dengan kuadrat sempurna, sehingga rumus yang harus dihafalkan jadi lebih sedikit.
dengan kuadrat sempurna, sehingga rumus yang harus dihafalkan jadi lebih sedikit.
Rumus:
tau
- LATIHAN SOAL
- 1. Diberikan persamaan lingkaran:
L ≡ x2 + y2 = 25.
Tentukan persamaan garis singgung lingkaran yang memiliki titik singgung di (−4, 3).
Pembahasan
Menentukan garis singgung pada suatu lingkaran yang pusatnya di (0, 0) dan diketahui titik singgungnya.
Lingkaran L ≡ x2 + y2 = r2
Titik singgung (x1, y1)Persamaan garis singgungnya adalah:

Dengan x1 = − 4 dan y1 = 3, persamaan garisnya:
−4x + 3y = 25
3y −4x − 25 = 02. Persamaan garis singgung lingkaran x2 + y2 − 6x + 4y − 12 = 0 di titik (7, 1) adalah….
A. 3x − 4y − 41 = 0
B. 4x + 3y − 55 = 0
C. 4x − 5y − 53 = 0
D. 4x + 3y − 31 = 0
E. 4x − 3y − 40 = 0
(un 2011)
Pembahasan
Data soal:
L ≡ x2 + y2 − 6x + 4y − 12 = 0
A = −6
B = 4
C = − 12
(7, 1)
x1 = 7
y1 = 1
Rumus sebelumnya, diperoleh garis singgung lingkaran:
 3. Diberikan persamaan lingkaran:
3. Diberikan persamaan lingkaran:
L ≡ (x − 2)2 + (y + 3)2 = 25
Tentukan persamaan garis singgung lingkaran dengan titik singgung pada (5, 1).
Pembahasan
Persamaan garis singgung pada lingkaran:L ≡ (x − a)2 + (y − b)2 = r2pada titik singgung (x1, y1)

dengan
a = 2 dan b = −3 dan r2 = 25
maka persamaan garisnya
 4. Persamaan garis singgung pada lingkaran x2 + y2 − 2x + 4y − 220 = 0 yang sejajar dengan garis 5 y + 12x + 8 = 0 adalah...
4. Persamaan garis singgung pada lingkaran x2 + y2 − 2x + 4y − 220 = 0 yang sejajar dengan garis 5 y + 12x + 8 = 0 adalah...
A. 12 x + 5y − 197 = 0 dan 12x + 5y + 195 = 0
B. 12 x + 5y + 197 = 0 dan 12x + 5y − 195 = 0
C. 5 x + 12y + 197 = 0 dan 5x + 12y + 195 = 0
D. 5x + 12y − 197 = 0 dan 5x + 12y − 195 = 0
E. 12 x − 5y − 197 = 0 dan 12x − 5y + 195 = 0
Pembahasan
Lingkaran x2 + y2 − 2x + 4y − 220 = 0 memiliki pusat:

dan jari-jari

Gradien garis singgungnya sejajar dengan 5 y + 12x + 8 = 0, jadi gradiennya adalah −12/5.
Persamaannya:

Sehingga dua buah garis singgungnya masing-masing adalah
 5. Persamaan garis singgung lingkaran x2 + y2 − 4x + 2y − 20 = 0 di titik (5, 3) adalah....
5. Persamaan garis singgung lingkaran x2 + y2 − 4x + 2y − 20 = 0 di titik (5, 3) adalah....
A. 3x − 4y + 27 = 0
B. 3x + 4y − 27 = 0
C. 3x + 4y − 27 = 0
D. 7x+ 4y − 17 = 0
E. 7x + 4y − 17 = 0
(UN 2005)
Pembahasan
Titik singgung : (x1, y1)
pada lingkaran : L ≡ x2 + y2 + Ax + By + C = 0
Rumus garis singgungnya:
Data:
x2 + y2 − 4x + 2y − 20 = 0
Titik (5, 3)
A = −4
B = 2
C = − 20
x1 = 5
y1 = 3
Garis singgungnya: Masih bingung?! Tenang saja! Ada video yang bisa membantusumber : http://tomyherawansman48jkt.blogspot.co.id/2015/06/persamaan-lingkaran-lingkaran-dengan.htmlhttps://matematikastudycenter.com/kelas-11-sma/158-persamaan-garis-singgung-lingkaran-sma
Masih bingung?! Tenang saja! Ada video yang bisa membantusumber : http://tomyherawansman48jkt.blogspot.co.id/2015/06/persamaan-lingkaran-lingkaran-dengan.htmlhttps://matematikastudycenter.com/kelas-11-sma/158-persamaan-garis-singgung-lingkaran-sma



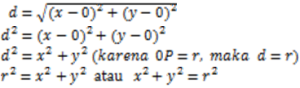
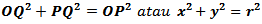
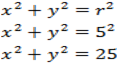
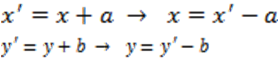
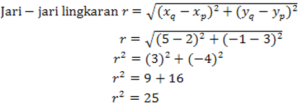
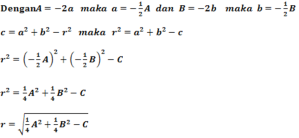

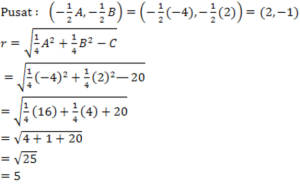
.png)

Komentar
Posting Komentar